Lecture 27—Wednesday, November 28, 2012

Topics

• Fitting the models from last time
• Checking the fit of logistic regression model
  • The Pearson test
  • The residual deviance test
  • A parametric bootstrap implementation of the residual deviance test
• Overdispersion and the quasi-binomial model
• Logistic regression with continuous predictors
• Interpreting the coefficients of logistic regression
  • Interpretations on a logit scale
  • Interpretations on a probability scale
  • Interpretations as odds ratios
• Confidence intervals for odds ratios
  • Odds ratios for sewers: yes versus no
  • Odds ratio for high intensity land use versus rural land use
  • Odds ratio for mixed land use versus rural land use
• Odds ratio interpretations for continuous predictors
• Cited references
• R code

R functions and commands demonstrated

• df.residual extracts the degrees of freedom of the residual deviance from a glm model.
• deviance extracts the residual deviance from a glm model.
• rev reverses the order of the elements of a vector.

Fitting the models from last time

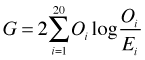
I reload the wells data set, collapse landscape categories, and fit the final model from last time.

Checking the fit of logistic regression models

Just as with Poisson regression, the fitted and predict functions can be used to apply the regression equation to individual observations. The predict function returns values on the scale of the link function, here the logit, while the fitted function undoes the link function and returns values on the scale of the response, here as probabilities.

We can also obtain the probabilities from predict if we specify the type='response' argument.

The mean number of counts for each binomial observation can be obtained by multiplying the fitted probabilities by the total number of trials for that observation.

The Pearson test

Because binomial data are categorical we can use a categorical goodness of fit test such as the Pearson chi-squared statistic to check the fit of the model. The observed data are the number of contaminated and uncontaminated wells out of n for each site. Thus to carry out the goodness of fit test we need to calculate both the estimated number of successes and the number of failures for each site. I assemble them in a matrix.

In a similar fashion I assemble the observed number of successes and failures in a matrix of the same dimension.

There are actually too many small predicted counts for the chi-squared distribution of the Pearson deviance to be valid.

I carry out the Pearson test anyway.

Although our Pearson statistic is calculated using 40 different values from a 20 × 2 matrix, the values are not independent. We know how many wells there are in each stratum. If these are really grouped binary data this number was chosen by us and is not random. The only thing that is random is how the wells are allocated to the two categories. Once we know how many wells are in the contaminated category we immediately know how many uncontaminated wells there were at that site by subtracting from the total. Thus we have n = 20 free values, one from each stratum. There are no further constraints arising from the study design. The degrees of freedom of the test is therefore n – p = 16, the number of binomial observations, n = 20, minus the number of estimated parameters, p = 4.

So if the p-value of this test can be trusted we have no evidence for lack of fit.

The residual deviance test

The residual deviance of the model is another potential goodness of fit test for grouped binary data (but not binary data). Again it's probably inappropriate here because of the large number of small predicted counts. The residual deviance and its degrees of freedom appear at the bottom of the output from the summary function.

Deviance Residuals:
   Min      1Q  Median      3Q     Max 
-1.631  -1.195  -0.185   0.668   1.717 

Coefficients:
               Estimate Std. Error z value Pr(>|z|)   
(Intercept)      -1.725      0.299   -5.76  8.2e-09 ***
land.use4mixed   -1.050      0.237   -4.42  9.7e-06 ***
land.use4rural   -2.945      0.742   -3.97  7.2e-05 ***
seweryes          1.541      0.288    5.35  8.9e-08 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 146.956  on 19  degrees of freedom
Residual deviance:  21.502  on 16  degrees of freedom
AIC: 74.78

Number of Fisher Scoring iterations: 5

We can also extract the deviance and its degrees of freedom directly from the model with the deviance and df.residual functions or by specifying the $deviance and $df.residual components of the model. Like the Pearson statistic, the deviance also has a large-sample chi-squared distribution.

So the residual deviance test agrees with the Pearson test. We have no evidence of lack of fit. The residual deviance test is the same as the G-test, which is asymptotically equivalent to the Pearson test.

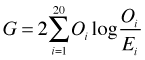
Using the formula as written directly on these data is not possible because some of the observed counts are zero which would force us to take the log of zero which is undefined. To get around this we use a result from calculus that

So, the zero counts should contribute nothing to the statistic.

We can also calculate the residual deviance by hand. Suppose we fit a saturated model to these data, a model with one parameter per observation. One way to obtain a saturated model is to fit a model with the original land.use variable, the sewer variable, and their interaction.

Alternatively we can create a new factor variable with 20 levels and use it as the only predictor in the model.

Next calculate the likelihood ratio statistic that compares the current model, out2d, against the saturated model.

Once again we get the value that is reported as the residual deviance of our current model. The residual deviance is reported routinely for all models fit using the glm function. It always means the same thing. It's the likelihood ratio statistic that compares the current model against a model that has one parameter for every observation and hence fits the data perfectly. The residual deviance is an attempt to place the log-likelihood of a model on some kind of absolute scale.

Observe that even though glm reports the residual deviance and its degrees of freedom, it doesn't report a p-value. The connection between the residual deviance and the G-test (and hence the Pearson test) suggests that using it as a goodness of fit statistic really only makes sense for count data and hence for data that might be modeled using a Poisson or binomial distribution. For instance, the residual deviance is totally inappropriate for assessing model fit with binary data. Furthermore, because of its connection to the Pearson test the size of the expected cell counts is an issue. If the the fraction of small expected cell counts is high, say greater than 20%, the residual deviance cannot be assumed to have a chi-squared distribution with n – p degrees of freedom. This is a potential problem here where 32.5% of the expected counts are small. Small expected counts are common with real data and so the residual deviance should not be routinely used to check model fit.

A parametric bootstrap implementation of the residual deviance test

The problem with both the residual deviance (G-test) and the Pearson test for these data is the large number of small expected counts. As a result we can't be sure that either statistic has a chi-squared distribution and therefore the calculated p-value is suspect. An alternative to assuming a chi-squared distribution is to generate a null distribution for the residual deviance ourselves using the parametric bootstrap. The parametric bootstrap was discussed previously (lecture 6). The idea is simple. We use the model whose fit we wish to test to generate a new response variable for each observation. Treating this simulated response as the actual response we then refit the model and calculate a goodness of fit statistic. We do this repeatedly thereby building up a frequency distribution for the goodness of fit statistic, a distribution of likely values we'd expect to see when the model actually fits the data. We then compare the actual goodness of fit statistic to this distribution to see if it looks in anyway unusual. If it does we have evidence of lack of fit.

I set this up as a function that carries out one complete step of this process. The function calculates both the Pearson statistic and the G-test (residual deviance) statistic, although in practice we would only calculate one. It returns the residual deviance.

I implement this 999 times and then add the actual residual deviance as one additional simulation. I then count up the number of simulated values that are as large as or larger than the actual residual deviance. When that's divided by 1000 we have a simulation-based p-value for the residual deviance goodness of fit test.

The simulation-based result match our conclusions based on a chi-squared distribution for the test statistic. We fail to find evidence of lack of fit.

Overdispersion and the quasi-binomial model

I need to comment on a frequently used seat of the pants rule about the residual deviance that is promulgated in textbooks and articles about statistics written for ecologists. The rule suggests that we calculate the ratio of the residual deviance to its degrees of freedom.

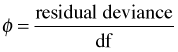
If φ > 1 we say the data are overdispersed relative to a binomial distribution. If φ < 1 we say the data are underdispersed relative to a binomial distribution. (Similar statements apply to count data that are assumed to follow a Poisson distribution.) For the current data set and model we find

so we would say based on the fitted model that the data are overdispersed relative to a binomial distribution, meaning that the data show more variability than is predicted by a binomial distribution.

Technically speaking it's not the deviance based on the G-statistic that is usually used for assessing over- or underdispersion, but instead it is the "deviance" based on the Pearson goodness of fit statistic. If we calculate the Pearson statistic for this model using all 20 categories including both the successes and failures we obtain the following.

This is a slightly smaller value than the value of φ we obtained using the residual deviance but once again φ > 1 so we would say the data are overdispersed relative to a binomial distribution.

If Y has a binomial distribution with parameters n (number of trials) and p (probability of a success) then theory tells us that

If the data are overdispersed or underdispersed relative to a binomial distribution then the rule says we need to correct for this in some way. One approach is to multiply the estimated binomial variance by φ yielding what's called a quasi-binomial model. (There is a comparable quasi-Poisson model.)

A quasi-binomial model can be fit directly with the glm function in R by specifying family=quasibinomial.

Deviance Residuals:
    Min       1Q   Median       3Q      Max 
-1.6314  -1.1947  -0.1846   0.6685   1.7167 

Coefficients:
               Estimate Std. Error t value Pr(>|t|)   
(Intercept)     -1.7252     0.3253  -5.304 7.13e-05 ***
land.use4mixed  -1.0497     0.2580  -4.069 0.000893 ***
land.use4rural  -2.9445     0.8061  -3.653 0.002145 **
seweryes         1.5408     0.3132   4.920 0.000154 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for quasibinomial family taken to be 1.181510)

    Null deviance: 146.956  on 19  degrees of freedom
Residual deviance:  21.502  on 16  degrees of freedom
AIC: NA

Number of Fisher Scoring iterations: 5

In the summary output R reports a dispersion parameter of 1.181510 which we recognize to be the Pearson deviance divided by the residual degrees of freedom that was calculated above. Notice that the AIC value is reported as missing, NA. That's because we no longer have a likelihood-based model, hence no log-likelihood and no AIC are calculated (but see Burnham and Anderson 2002 for something they call QAIC). The quasi-binomial model is not an actual probability model. It is just a post hoc adjustment to the variance of the binomial distribution.

We should compare the coefficient tables of the binomial and quasi-binomial models to see what's changed.

Observe that the parameter estimates of the two models are exactly the same, but the standard errors and hence the statistical tests are different. All that's happened is that the variances of the parameter estimates in the binomial model have been multiplied by the estimate of φ, the Pearson deviance divided by the degrees of freedom.

The overdispersion parameter has been used to increase the standard errors of the parameter estimates. This in turn has decreased the z-statistics and increased the p-values making it harder to achieve statistical significance.

So, is fitting a quasi-binomial a good idea? Generally speaking I would say no.

1. Because of its connection to the G- and Pearson tests that do have minimum expected count guidelines, the residual deviance is only rarely an appropriate goodness of fit statistic. Hence φ is rarely estimating anything sensible.
2. The variance assumption that is made with a quasi-binomial model is fairly restrictive. Without further evidence there is no reason to believe that this adjustment is better than doing nothing at all.

If there is overdispersion with binomial data it means that the current binomial model is inappropriate. The binomial model might be inappropriate because we haven't found an appropriate set of predictors to describe the logit or because one or more of the assumptions of the binomial distribution have not been met. Therefore one recommendation when there is overdispersion is to include more predictors in the model if possible. Two assumptions of the binomial distribution that are commonly violated with real data are independence and the constant probability of success for all of the Bernoulli trials that comprise the individual binomial responses. One way to account for both of these violations is to fit a binomial mixed effects model. This yields a true probability model that can be estimated using maximum likelihood and thus provides an AIC for model comparison. A mixed effects binomial model will typically yield parameter estimates and standard errors that are different from those of the ordinary binomial model. I think this approach is preferable to just trying to "patch" the variance of a binomial distribution in a very ad hoc manner.

Still, fitting a quasi-binomial model may be preferable to doing nothing. Because it inflates the reported standard errors (when there is overdispersion) the result is that all of your test results are made more conservative making it less likely for them to achieve statistical significance. This in turn adds a facade of objectivity to the analysis because you've chosen to set the statistical significance bar a bit higher. If I've exhausted all other possibilities—I can't find any more predictors to add to the model and a mixed effects model does not adequately address the problem—then and only then would I consider fitting a quasi-binomial model and using it as my final analysis.

Underdispersion with binomial data also means that the current binomial model is inappropriate but for different reasons. Once again there is heterogeneity in the success probabilities within the sets of Bernoulli trials but of a very limited form yielding "binomial" count distributions that have a far more limited range of possible outcomes. Underdispersion is far less common and as such there are far fewer tools available for dealing with it if it can be detected. This doesn't mean that fitting a quasi-binomial model is the best choice. If it turns out that the quasi-binomial model for underdispersion is correct but you instead choose to fit a binomial model anyway, no real damage is done. It just means that your reported statistical tests are too conservative. Any result that ends up being statistically significant with the binomial model will still be statistically significant with the correct quasi-binomial model, but there may be other statistically significant effects that you failed to detect.

Logistic regression with continuous predictors

There are two continuous predictors in the data set, chloride and nitrate. I try adding them to a model that is additive in the sewer and the three-category land use variable.

AIC would suggest that adding nitrate to the model has improved the model, but that the chloride variable is not needed. I test this with a likelihood ratio test.

Model 1: cbind(y, n - y) ~ land.use4 + sewer
Model 2: cbind(y, n - y) ~ land.use4 + sewer + nitrate
  Resid. Df Resid. Dev Df Deviance P(>|Chi|) 
1        16     21.502                       
2        15     17.044  1   4.4581   0.03474 *
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

So the likelihood ratio test is in agreement with AIC.

Although we've been using AIC to rank models the truth is we only have n = 20 binomial observations, so no matter how many parameters we estimate. Because we're now fitting models with four and more parameters we should probably be using corrected AIC, AIC_c, for model comparison. One problem with this idea is that it's not clear that AIC_c is appropriate for non-normal models (as has been noted before). It's also not clear what to use for n here. Do we count the 20 independent binomial observations or the 650 binary observations (assumed independent) that make up the binomial data?

Interpreting the coefficients of logistic regression

Interpretations on a logit scale

The coefficients of a logistic regression model have exactly the same interpretation as do ordinary regression coefficients except that they are describing the effect of predictors on a response measured on a logit scale.

The regressors in the current model are all dummy variables so the different coefficients tell us how much the logit changes if we switch from the reference category (land.use4 = "high.use" and sewer = "no") to a different category.

• The intercept, –1.72, is the value of the logit for the reference category: sewer = "no"and land.use4 = "high.use".
• The mixed coefficient is how much the logits of the mixed and high use categories differ. The mixed use category has a logit that is 1.05 units lower than is the logit of the high use category.
• The rural coefficient is how much the logits of the rural and high use categories differ. The rural use category has a logit that is 2.94 units lower than is the logit of the high use category.
• The sewer coefficient tells us that wells on a site with sewers have a logit that is 1.54 units higher than wells that are on a site without sewers.

Interpretation on a probability scale

Each coefficient except for the intercept measures an effect, the amount the logit will change when we switch categories. Because the logit function is an invertible monotonic transformation of probability, the direction in which the logit changes is also the direction in which the probability of contamination will change. The sign of the predictor in a logit regression model gives this direction. Thus we see that wells on sites of mixed use have a lower probability of contamination than those in high use areas. Similarly wells in rural areas have a lower probability of contamination than wells in high use areas. Wells in areas with sewers have a higher probability of contamination than wells in areas without sewers.

Interpretation as odds ratios

One of the primary appeals of logistic regression is that the coefficients of dummy predictors have a connection to odds ratios. As an illustration, suppose our model just included a dummy variable z for sewer where z = 0 if sewers our absent and z = 1 if sewers are present. The basic logistic regression model is the following.

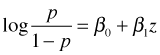
As with ordinary regression this single equation corresponds to two equations depending on the value of the dummy variable z.

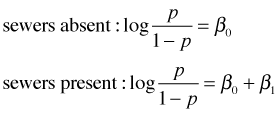
As was explained in lecture 26, the logit is a log odds, so our two equations also have the following interpretations.

If we subtract the first equation from the second equation the intercept term cancels.

It is a property of logarithms that a difference of two logarithms is the logarithm of a quotient.

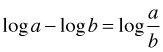
Thus the difference of the two log odds is also the log of a ratio of odds where the reference group appears in the denominator.

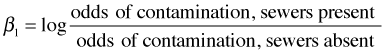
If we exponentiate both sides of this equation the log disappears and the right hand side is just a ratio of odds, an odds ratio, usually denoted OR.

An odds ratio interpretation for the coefficients of a set of dummy variables applies no matter how many levels there are. Exponentiating a coefficient of a dummy variable in a logistic regression model yields an odds ratio in which the reference group occupies the denominator of the odds ratio. In the current model there are two factor variables, one with three levels and one with two. The reference group for land.use4 is "high.use" and the reference group for sewer is "no".

Exponentiating the "effect" estimates yields odds ratios with the following interpretations.

• The odds of well contamination in mixed use areas is 35% that of the odds of contamination in high use areas.
• The odds of well contamination in rural areas is 5% that of the odds of contamination in high use areas.
• The odds of well contamination when sewers are present is 4.7 times the odds of contamination when sewers are absent.

It is convenient particularly when constructing confidence intervals to arrange things so that point estimates for odds ratios are bigger than one. Recall the following property of logarithms.

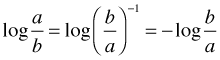
When we change the sign of a log odds ratio we get the reciprocal of the ratio thus changing the reference category. If we put a minus sign in front of the coefficient labeled land.use4rural, the rural category becomes the denominator of the odds ratio and the current reference group high.use becomes the numerator.

The odds of well contamination are 19 times higher in high use areas than they are in rural areas. Changing the sign of the coefficient labeled land.use4mixed makes the mixed use category the reference group.

So the odds of well contamination in high use areas are 2.86 times the odds of contamination in mixed use areas.

With the current coding of the model we can only obtain odds ratios that compare high use with rural and high use with mixed. How do we compare rural with mixed use? We could refit the model with a different reference group but it is just as easy to obtain this comparison using what we already have. The model we've fit is the following.

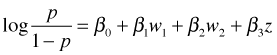
where

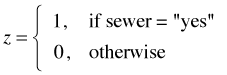
so the reference group is land.use4 = high.use and sewer = no. The modeled response is the log odds of contamination. The regression model yields three different equations, one for each category of land use.

1. High intensity land use:
2. Mixed land use:
3. Rural land use:

If we subtract eqn (3) from eqn (2) the intercept and the sewer term will cancel (assuming that sewer status is the same in both equations).

Exponentiating this yields the odds ratio. So, to obtain an odds ratio that compares two groups not currently being compared, just subtract their exponents. The group corresponding to the term with the minus sign (the subtrahend) forms the denominator of the odds ratio.

Alternatively we could have just recoded the land use factor and made rural the reference group. I accomplish this below by reversing the current factor level order with the rev function.

These are the same values obtained above by subtracting coefficients.

Confidence intervals for odds ratios

An odds ratio is a derived quantity, a function (the exponential) of a regression coefficient or a linear combination of regression coefficients from a logistic regression model. Because the estimates in a logistic regression model are obtained by maximum likelihood, likelihood theory tells us they should have a large-sample normal distribution. So normality holds on the scale of the estimates and we can use that to calculate confidence intervals. The exponential function is monotonic so it preserves order. Hence when we apply it to a 95% confidence interval on the logit scale we get a 95% confidence interval on the odds ratio scale. Exponentiating the point estimate gives the odds ratio and exponentiating the endpoints of this interval yields a confidence interval for the odds ratio.

Let's start with the odds ratios we can calculate from model out2d. The fitted model is

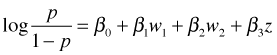
As was noted above, confidence intervals for odds ratios are easier to interpret when the point estimate for the odds ratio is bigger than 1. With this in mind suppose we are interested in finding confidence intervals for the following three odds ratios.

1. Odds ratio for contamination, sewers present versus sewers absent:
2. Odds ratio for contamination, high land use versus rural land use:
3. Odds ratio for contamination, mixed land use versus rural land use:

I start by extracting the coefficients table from the summary table of the model.

We can also obtain confidence intervals for these parameters with the confint function.

Odds ratio for sewers: yes versus no

A 95% confidence interval for the sewer coefficient β₃, using the asymptotic normality of MLEs, is the following.

Exponentiating the point estimate gives the odds ratio. To obtain a confidence interval for the odds ratio we just exponentiate these two endpoints.

Alternatively we can exponentiate the fourth row of the output from confint.

The numbers are not the same because confint uses profile likelihood to obtain the confidence intervals while the hand calculations we carried out produced Wald confidence intervals.

Odds ratio for high intensity land use versus rural land use

A 95% confidence interval for the rural coefficient β₂ can be obtained by again invoking the asymptotic normality of MLEs.

Next we flip the signs and exponentiate the results.

Alternatively we can exponentiate the negative of the third row of the output from confint. (Notice that because we changed the sign the labeling of the interval endpoints is backwards.)

Odds ratio for mixed land use versus rural land use

From eqn (3) the estimate of the log odds ratio is obtained by subtracting two regression coefficients, β₁ – β₂. This is also an instance of a linear combination. The general problem of finding the variance of a linear combination of regression coefficients was discussed in lecture 4. Those same ideas apply here. We need to write this linear combination as a vector dot product using the full vector of regression coefficients. The dot product we need is the following.

As was explained in lecture 4 the variance of a linear combination can be obtained by evaluating the following quadratic form.

where and is the variance-covariance matrix of the parameter estimates returned by the vcov function of R applied to the model object. Thus the standard error of the desired log odds ratio is the following.

Using the point estimate and its standard error we can calculate a 95% confidence interval for the log odds ratio as follows.

The rationale for this is that maximum likelihood estimates have a joint asymptotic normal distribution. Sums of jointed normally distributed variables also have normal distributions. The strategy then for finding a confidence interval for an odds ratio is to first find a confidence interval for the linear combination of regression coefficients and then exponentiate the endpoints of this interval to obtain a confidence interval for the odds ratio.

To obtain this interval using confint we'd need to refit the model making rural the reference group. We previously did this creating a model I called out2f.

The three odds ratios we calculated and their confidence intervals are listed in Table 1.

The width of the confidence intervals is striking, particularly the long upper tail. This is typical for ratios where imprecision in the denominator gets magnified into large values for the ratio.

Odds ratio interpretation for continuous predictors

All of the interpretations we've given for the coefficients of categorical regressors in logistic regression carry over to continuous predictors. Suppose x is a continuous predictor and we fit the following logistic regression model.

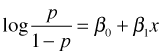
Now consider this equation for any two values of x that differ by one unit.

Subtract the first equation from the second equation.

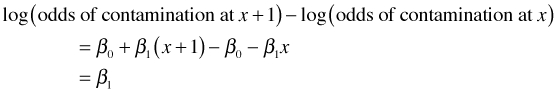
Because the difference of two logs is the log of a ratio the regression coefficient β₁ is also a log odds ratio.

Exponentiating the regression coefficient yields the odds ratio of contamination for a one unit increase in x. Consider model2i in which the continuous predictor nitrate was added to a logistic regression model with two categorical predictors.

The coefficient of nitrate has the following three interpretations.

1. A one unit increase in nitrate concentration increases the logit by 0.27.
2. Because the coefficient of nitrate is positive we conclude that increasing the concentration of nitrate increases the probability that a well is found to be contaminated.
3. A one unit increase in nitrate multiplies the odds of contamination by a factor of 1.31.

We're not restricted to one unit increases. A k-unit increase in x yields an odds ratio of exp(kβ).

Cited references

• Burnham, K. P. and D. R. Anderson. 2002. Model Selection and Multimodel Inference. Springer-Verlag, New York.

R Code

A compact collection of all the R code displayed in this document appears here.

Course Home Page