. D is called the spatial domain and will usually be a subset of the Cartesian plane. In data analysis there are two basic approaches to dealing with spatially referenced data and they influence what our sample size is.Formally spatial data entail recording an attribute’s value, z, along with the attribute’s location, s. We represent this as Z(s), where typically . D is called the spatial domain and will usually be a subset of the Cartesian plane. In data analysis there are two basic approaches to dealing with spatially referenced data and they influence what our sample size is.
In the nuisance point of view spatial correlation reduces our ability to draw valid inferences from our data. In a typical statistical experiment, say a simple linear regression, we manipulate the levels of a variable x of different experimental units while observing the value of a second variable y (that we call the response). But in an observational study, which we carry out because an experiment might be too difficult to perform or too unrealistic, we often use the natural variability in x as a surrogate for experimental manipulation. The natural variability is captured by obtaining observational units from different spatial locations. What does such a study allow us to conclude? Because we didn't randomly assign treatments to we can't legitimately infer that x causes y. Furthermore if x and y are seen to vary together it could be because an unmeasured spatially varying variable is affecting both of them.
Spatial location can serve as a catch-all for all the unmeasured variables in an analysis. Tobler’s law of geography (Tobler 1970) states “Everything is related to everything else, but near things are more related than distant things.” So we expect the spatial dimension to be important in most observational studies.
Three distinct categories of spatial data are recognized: geostatistical data, lattice data, and point process data (spatial point patterns).
The spatial domain D here is fixed and continuous. With geostatistical data the number of locations at which observations can be made is uncountable. Between any two sample locations si and sj are an infinite (in theory) number of other potential sample points. How we choose to obtain a sample from D has no bearing on whether the data are geostatistical or not. We can lay down a grid and sample at the intersection of grid lines, or we can randomly select points. Furthermore the attribute we measure, Z(s), can be categorical or continuous.
Here the set D is fixed but this time is only countable (and usually finite). Lattice data are sometimes called areal data. Examples of lattice data include the following.
Because lattice data have areal extent there is no way to obtain additional sample points between contiguous lattice units.
Unlike geostatistical and lattice data the domain D for point process data is random. With point process data the focus is on the locations at which the process occurs. The set of spatial locations of a plant species, i.e., the places where the plant species is observed to grow, is an example of a point process. Instead of analyzing the Z process (the attributes of the points) we analyze the D process (the locations of the points). Having said that it is possible for the points to have additional attributes yielding what's called a marked point process.
Geostatistical → point process. Geostatistical data under certain circumstances can be treated as point process data. Suppose we define
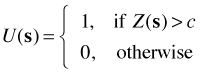
Now suppose we record the locations where U(s) = 1. These locations are clearly random and comprise a point process data set.
Geostatistical → lattce. We can choose to aggregate geostatistical data by area and summarize the results over the area thus generating lattice data.
Lattice → geostatistical. Going from lattice to geostatistical data is harder. Typically we have to pretend that the value of Z(s) on a lattice occurs at the center of the lattice units and then treat D as if it were continuous so that intermediate values are possible.
Point process data
Geostatistical data
Lattice data
The variance, denoted 
or 
to emphasize the identity of the variable in question, is the average squared deviation about the mean.
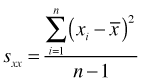
An equivalent formula is the following.
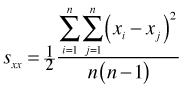
In this formula the variance is the average squared differences among all pairs of observations. The multiplier of one half accounts for the fact that the double sum counts each of these squared differences twice. Many spatial statistics use versions of this second variance formula.
The covariance generalizes the variance to the case of two variables measured on each observation. The covariance quantifies the direction and extent to which the two variables co-vary on average.
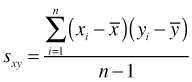
To improve interpretability the covariance is often standardized by dividing it by the product of the square root of the variances of each variable. This yields the Pearson correlation coefficient r, which has a range of –1 to 1.
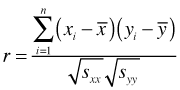
As we'll see these formulas can be extended in various ways with spatial data.
One of the purposes of a spatial analysis is to characterize the nature of the spatial process. This is made difficult by the fact that technically we have no replication of the process. A sample of a spatial process is a sample of size one regardless of how many spatial locations we've measured. Spatial data are like multivariate non-spatial data in which we obtain multiple measurements on the same individual. But spatial data pose a unique problem not shared by non-spatial data.
The standard "solution" is to substitute replication in the data for replication of the data. An assumption that is made in spatial analysis is that the spatial process under study repeats itself over its domain D. Such a spatial process is said to be stationary. For a stationary process the absolute coordinates at which we observe the process are unimportant. All that matters are the orientated distances between the points. If in addition the process is invariant to the direction of the displacement in that only the magnitude of the displacement matters, then the process is said to be isotropic.
In a stationary process if we translate the entire set of coordinates by a specific amount in a specified direction, the entire process remains the same. This is the same assumption we make in time series analysis in order to estimate lag correlations over the entire time series.
The proper way to view spatial data is as multivariate data. Suppose we observe a spatial process at locations s1, s2, ..., sk. The behavior of the spatial process Z(s) can be completely characterized by its joint probability distribution function.
A very strong form of stationarity is one that requires that the joint probability distribution function be invariant under translation. Let h be any displacement vector. Formally strong stationarity is defined as follows.
For most applications strong stationarity is too restrictive a requirement. A weaker form of stationarity requires only that the moments of the joint distribution don’t change under translation. This is called second-order stationarity. Formally two conditions are required for second-order stationarity.
for all locations s in D. 
for all locations s. C*(h) is called the covariogram. It is a function that depends only on the displacement vector h.If it turns out 
, where 
is the norm of the vector h, so that the covariance depends on the size of the displacement but not on its direction from s, the spatial process is said to be both second order stationary and isotropic.
A technique often used in time series analysis to remove absolute time references and to obtain stationarity is differencing, i.e., constructing the new variable Z(s) – Z(s+h). This leads to a third definition of stationarity, intrinsic stationarity. Formally a spatial process is intrinsic stationary if it has a constant mean and the variance of the differences of Z at pairs of locations only depends on h, the displacement between the locations. This leads us to the definition of the semivariogram, γ(h).
Because it derives from the weakest form of stationarity and is more generally applicable, the semivariogram is the preferred tool for characterizing geostatistical spatial processes.
Although the semivariogram is less intuitive than the covariogram, it turns out the two are related and so it is easy to move from one to the other. If an intrinsic stationary process has the additional property of second-order stationarity, then the covariogram C(h) and semivariogram γ(h) are related as follows.
By definition C(0) is just the variance of the spatial process.
Note: the terms semivariogram and variogram are often used interchangeably in the literature. Technically the semivariogram is as defined above, while the variogram is twice this quantity. The reason the distinction is important is that the semivariogram has the nice relationship to the covariogram shown above. Typically when someone speaks of the variogram (particularly in software documentation) they are actually referring to the semivariogram.
Tobler, W. 1970. A computer movie simulating urban growth in the Detroit region. Economic Geography 46: 234–240.
| Jack Weiss Phone: (919) 962-5930 E-Mail: jack_weiss@unc.edu Address: Curriculum for the Environment and Ecology, Box 3275, University of North Carolina, Chapel Hill, 27599 Copyright © 2012 Last Revised--March 28, 2012 URL: https://sakai.unc.edu/access/content/group/2842013b-58f5-4453-aa8d-3e01bacbfc3d/public/Ecol562_Spring2012/docs/lectures/lecture30.htm |
